Billiam | Water System

Overview

This is an overview of my Water System for Unity, summarising the techniques I used to try and create a fully-featured, realistic ocean for use in my own games. As it turns out, oceans in games are extremely complex and multifaceted systems with strict performance requirements. Note that my resources are linked throughout and at the bottom of the page.

Setup

Before starting work on any shaders, I first implemented a system to generate a subdivided plane mesh and draw it to the screen via a custom render pass. This is handled by a singleton 'WaterSystem' object, while the 'WaterSurface' component can be created and modified in the scene. Next, I implemented a pre-rendering step to handle compute shader execution via a command buffer. By design this setup mirrors Unity's own HDRP water system, which requires no additional components or render passes to be manually added.
To run my pre-render function, I hook into the per-camera rendering callback like so:

RenderPipelineManager.beginCameraRendering += RenderSurface;

And fetch a command buffer using CommandBufferPool.Get():

void RenderSurface(ScriptableRenderContext context, Camera camera)
{
    CommandBuffer commandBuffer = CommandBufferPool.Get("Water CMD");
    
    UpdateSurface(waterSurface, commandBuffer, context, camera);
    
    context.ExecuteCommandBuffer(commandBuffer);
    context.Submit();

    commandBuffer.Clear();
    CommandBufferPool.Release(commandBuffer);
}

The 'UpdateSurface' updates the simulation state for the ocean surface, caustics and cutouts as well as enqueues the necessary render passes.

Wave Displacement

In previous attempt at water shading, I had used used a shader graph to displace vertices using the sum of Gerstner Waves. While this looked acceptable over a small area, the further you can see into the horizon the easier it was to see the waves repeating over and over. So how do games like Sea of Thieves create their vast and stunning oceans?

One method utalizes the Fast Fourier Transform, explained and implemented here: I Tried Simulating The Entire Ocean. This technique has been popular in games and movies since it was proposed in the 2004 paper Simulating Ocean Water by Jerry Tessendorf, and I will attempt to explain it here.

What must be understood before understanding the Fourier Transform is that any periodic waveform can be identically reproduced with a sum of sinusoids. The purpose of Fourier Transform, is to take a waveform and decompose it into a sum of sinusoids resulting in a close approximation of that waveform.

The output of the Fourier Transform is a wave graph in the "frequency domain" which, as opposed to describing how amplitude at a given time (time domain), describes the amplitude of a wave at a given frequency. For example, for a wave of frequency 30hz we see a spike in the frequency domain at 30hz.

Time domain vs frequency domain. Figure from here

For water simulation, this process is performed in reverse, taking a signal in the frequency domain and converting it to the time domain (the Inverse Fourier Transform).
The initial frequency domain signal will control the 'look' of the ocean; how choppy are the waves, where are the predominant winds, etc. This signal can be generated in any way you like, which would likely result in some pretty wild looking oceans. However, luckily there are already methods for generating realistic ocean frequency spectra using models built from real-world wave data, such as the Phillips and JONSWAP spectra.

These wave spectra can represent tens of thousands of frequencies. At a resolution of 256x256, the IFT is performed over 65,000 times (once on each every pixel). To make this real-time compatable, the Fast Fourier Transform is used. The FFT uses a 'Butterfly Algorithm' to recursively split the input data in half which avoids unnecessary calculations. Please see here for a more in-depth exploration of the FFT.

Finally, the time domain is progressed which produces usable displacement and (derrived) slope maps which will be sent to the ocean shader.

However, even with very detailed wave spectra, the tiling issue is not yet completely eradicated. It is inevitable that any periodic waveform, or sum or periodic waveforms, will repeat given enough distance. However, the FFT is so fast we can actually compute several wave spectra simultaneously and scale them over the ocean surface. The millions of waves all interact and distort one another virtually eradicating tiling up to an extreme distance.

As one last trick I learned from HDRP is to define constants in a compute shader's kernals. I used to this give the user control over the resolution of the wave spectra and subsequent FFT passes as a graphics option.

#pragma kernel RowPass_128    FFTPass=RowPass_128                 FFT_RESOLUTION=128    BUTTERFLY_COUNT=7
#pragma kernel ColPass_128    FFTPass=ColPass_128   COLUMN_PASS   FFT_RESOLUTION=128    BUTTERFLY_COUNT=7
#pragma kernel RowPass_256    FFTPass=RowPass_256                 FFT_RESOLUTION=256    BUTTERFLY_COUNT=8
#pragma kernel ColPass_256    FFTPass=ColPass_256   COLUMN_PASS   FFT_RESOLUTION=256    BUTTERFLY_COUNT=8
#pragma kernel RowPass_512    FFTPass=RowPass_512                 FFT_RESOLUTION=512    BUTTERFLY_COUNT=9
#pragma kernel ColPass_512    FFTPass=ColPass_512   COLUMN_PASS   FFT_RESOLUTION=512    BUTTERFLY_COUNT=9

[numthreads(FFT_RESOLUTION, 1, 1)]
void FFTPass(uint3 id : SV_DISPATCHTHREADID)
{
    for (int i = 0; i < 8; i++)
    {
        #ifdef COLUMN_PASS
            _FFTTarget[uint3(id.xy, i)] = FFT(id.x, _FFTTarget[uint3(id.xy, i)]);
        #else
            _FFTTarget[uint3(id.yx, i)] = FFT(id.x, _FFTTarget[uint3(id.yx, i)]);
        #endif
    }
}

Water Shading

Next, I wrote a fragment shader to mimic the effects of light interacting with an ocean surface. My sources of light are the scene main directional light, an environmental cubemap as well as an optional setting for additional point/spot lights. Before I could get started, I first needed to understand the various reactions light undergoes when hitting water...
For any given ray of light hitting the ocean surface, we observe that several things can happen. It may reflected off the surface into the camera, resulting in a mirror reflection of the sky above. Or it may penetrate the ocean surface and then be scattered back out. Since red wavelengths more likely to be absorbed than scattered; we observe that areas of higher scattering the water appears lighter and more blue, areas of lower scattering are darker and more green. So, for any given fragment, I will attempt to approximate of how millions of light rays would interact with that part of the surface using a BRDF function.

In the GDC talk on Atlas mentioned above, see here, the developers present a Microfacet BRDF model, which consists of a Fresnel reflectance term, a normal distribution function and a masking function.
The Fresnel reflectance term describes areas where we will see scattered light vs reflected light, as well as specular highlights. It can be computed using the indices of refraction of air and water which, when viewed from under the surface, creates an effect called Snell's window. This describes how light exiting the ocean volume at a harsh angle totally internally refracted leading to a window above the camera where the sky can be seen, surrounded by an "opaque" surface.
The normal distribution function describes which direction relative to the normal vector of the surface incoming light is likely to reflect in.
And finally the masking term, or Geometric Attenuation term, the object self-shadowing as you view it at an increasingly perpendicular angle.

Finally, the developers use several "fudge terms" to mimic the likelihood of observing scattered light rays at any given part of the ocean:

An ambient term, we observe that some light is scattered uniformly.
A height term, we observe that more light is scattered in wave peaks.
A view term, we observe that we are more likely to see scattered light if the surface normal coincides with the view direction.
A shadow term, we observe that we are more likely to see scattered light if the surface normal coincides with the light direction.

All together that looks like this:

Surface Scattering + BRDF + Foam

Note that the FFT tiles are scaled up greatly, the normals can suffer from artefacts from the bilinear sampling. To fix this, I implemented a bicubic sampling method from Stack Overflow which creates a much smoother result at the cost of 4 times as many samples:

Dynamic Detail

Finally for the ocean surface, I needed to render the ocean mesh far into the horizon so the edge was not within the camera's far clipping plane. This cannot be achieved by simply tiling the dense grid mesh seen above, as that would result in millions of vertices taking up ever smaller amounts of screen space. Far better is to try and keep the vertex density of the ocean surface constant across the whole screen, reducing overdraw and limiting the vertex count. I used two techniqued to achieve this effect:

Dynamic LODs
Vertex Tessellation

Like using Levels of Detail to render decimated versions of objects as they get further from the camera, the same can be done to oceans only a little more complicated. Upon creating a HDRP ocean, three meshes are generated; a dense central grid, a rectangular grid mesh and a colossal outer mesh which is essentially a flat plane with a hole in it. These meshes are dynamically scaled and rotated to fill the surface.
Put together, the meshes look like this:

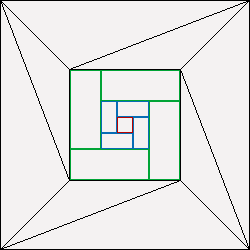
Red: dense grid, blue & green: rings, black: outer plane.

As the camera moves further away, the grid mesh expands to eclipse each layer of ring meshes, using the logarithm of the camera's height relative to the surface. When the camera is close to the surface, the grid mesh is made very small and 7 or so rings are drawn before the outermost plane. In contrast, at the maximum distance only the grid mesh and outer plane is drawn.

A neat optimisation here is to use indirect GPU instancing to draw the ring meshes since they are drawn dozens of times. This eliminates duplicate vertex batches by asking the GPU to cache the ring mesh and simply reuse it when requested. The instance ID is fetched in the vertex shader (before tessellation) and rotation and scaling data is applied from a Structured Buffer prepared beforehand. These meshes are frustum culled when generating the buffer, and again in the tessellation stage (per mesh and then per triangle).

Secondly, I implemented GPU Vertex Tessellation to generate more vertices on the GPU. In a tessellation shader, the distance from the vertex to the camera is used to generate a tessellation constant. This is used to recursively subdivide the ocean mesh, creating more displaceable geometry without sending it to the GPU with the rest of the scene.

Utilizing these methods allows the water to be depicted in extreme detail near the camera, while keeping the number of vertices sent to the GPU at just under 17k.

Underwater Rendering

With a convincing ocean surface as far as the eye can see, I could move on to the underwater effects. But I immediatly ran into a big problem; where on the screen is underwater and what is above water? For example; a camera can be situated well above the water, deep below it, or directly in it leading to a complex split in the screen where some is underwater and some is not.

My first attempt was to calculate the height at a given position from the displacement maps. However, this does not account for the horizontal component of the FFT's, or the limited resolution of the water mesh.

Next, I tried to recapture the height of the surface mesh after it is rendered using an orthographic camera above the view camera. Although multiple camera's does effect performance, this was able to produce a perfect waterline for a small area around the player. However, what if I wanted the player to be in a submarine where the waterline was not right infront of the camera, but a large window or the like?

My most recent attempt involves generating two masks; a position mask and a face mask. The face mask is captured to a render texture in a pre-pass, which renders the ocean surface before anything else using it's own depth texture. Front/back face information is stored in the red channel; front as 1.0, back as 0.5, leaving 0 where there is no surface present. To do this, I reused the pre-pass I had already implemented to capture the surface depth, which is useful for several underwater effects.

The position mask is computed using the position of the water surface and a position computed at the maximum depth from the camera using the screen space uv coordinates.
With these two masks, I can test if any given fragment is underwater with this logic:

bool ShouldRender(float2 uv, float sceneDepth)
{
    float surfaceMask = SAMPLE_TEXTURE2D(_SurfaceFaceMask, sampler_PointClamp, uv).r;

    if (surfaceMask > 0.9)
        return false;

    float3 skyboxPos = ComputeWorldSpacePosition(uv, 0.00001, UNITY_MATRIX_I_VP); // Tiny epsilon to remove line artefact created just under water plane.
    return surfaceMask > 0 || (_SurfacePosition.y > skyboxPos.y);
}

While this solution is far more performant than the orthographic camera method and can handle submarines, it does have a few issues that I'd like to address later. Most prominent is that violent waves can actually loop back around on themselved which creates backfaces above the water surface. These backfaces are improperly rendered as underwater. The last approach I have considered is using some sort of vertical smearing to propagate the lowest water surface pixels on the screen downwards. This would be performed in a compute shader after the depth pre-pass has been rasterized and, combined with the position mask, would create a perfect waterline so I may revisit this section later.

Finally with that done, I use the combined scene and water-surface depth textures to apply an absorption colour.

Caustics

To improve both the surface and underwater visuals, I implemented caustic patterns generated by the ocean surface. 'Caustics' refer to the patterns of light created when light rays exit one medium and enter another. As it does so, the light refracts - or bends - following the shape of the surface resulting in differing areas of high and low light density.

Many games achieve this by simply mapping a precomputed, animated texture to underwater geometry. This is a quick and dirty approach which is very effective for many games, especially those where the ocean waves are constant or performance is a large concern. However, it is possible to generate caustic patterns in real-time that actually reflect the state of the ocean surface, whether calm and slow or violent and stormy.

This article by Evan Wallace describes how this can be done by constructing a dense 'virtual plane' and refracting the vertices as if travelling through water. The new and old vertex positions are then ran through a ray, plane intersection function and given to the fragment shader. The colour of each fragment is then determined by the difference in area between the non-refracted plane and the refracted one, taking advantage of the fact that fragments are computed in sets of four. In Unity that looks like this:

float Frag (Varyings i) : SV_Target
{
    float intialTriangleArea = length(ddx(i.originalPos)) * length(ddy(i.originalPos));
    float refractedTriangleArea = length(ddx(i.refractedPos)) * length(ddy(i.refractedPos));

    return intialTriangleArea / refractedTriangleArea;
}

Which produces a texture like this:

This texture is closely fit to match the wave spectrum it is produced from. Since the FFT produces periodic textures, the caustics can be seamlessly tiled across the environment using a global uv system such as triplanar mapping.

Godrays

Godrays, or crepuscular rays, occur when light penetrates the water surface and is scattered outward, some of which travelling strait into your eyes. We can achieve this effect by utilizing the caustics texture we just computed, but rather than mapping it to the scene, we raymarch the texture as projected by the scene's Main Light:

float SampleGodrays(float3 positionWS, float3 lightDirection)
{
    float3 normal = float3(0.0, -1.0, 0.0);

    // Project caustics texture in light direction.
    float3 forward = refract(lightDirection, normal, 1.0 / _IndexOfRefraction);
    float3 tangent = normalize(cross(forward, float3(0.0, 1.0, 0.0)));
    float3 bitangent = cross(tangent, forward);

    float3 sampleCoord = positionWS * _TilingFactor;
    float2 uv = float2(dot(sampleCoord, tangent), dot(sampleCoord, bitangent)) * 0.5 + 0.5;

    // Sample caustics texture at a low LOD to blur away artefacts.
    return SAMPLE_TEXTURE2D_LOD(_CausticsTexture, sampler_LinearRepeat, uv, 5).r;
}

This is called from a raymarching function, including the usual upsampling and blur passes, before being composited onto the final image.

Water Cutouts

Finally, lets make the water interactable by implementing "dry cutouts" so that boats and submarines can displace the water. Games such as Subnautica and Atlas use Signed Distance Fields (SDF) to create complex shapes in which water is precluded from rendering.
An SDF essentially allows you to work out how far a given point is from the surface of a user defined shape. The distance is negative when the point is within the shape, and positive when it is outside. To produce an SDF that closely matches the hull of my submarine, I wrote a custom SDF generator which converts a mesh to a 3D texture where the red channel contains the distance from the surface. The generation algorithm first evaluates the bounds of the mesh, and then creates a texture with a user defined resolution to fit those bounds. Then, for each point in the 3D texture, the distance to every triangle in the mesh is evaluated and a value is updated every time a smaller distance is found.
This is performed within a compute shader, and looks like this:

float EvaluateTriangle(int triangleIndex, float3 pos)
{
    // a, b and c are the vertices of the triangle.
    float3 a = _Vertices[_Triangles[0 + triangleIndex * 3]];
    float3 b = _Vertices[_Triangles[1 + triangleIndex * 3]];
    float3 c = _Vertices[_Triangles[2 + triangleIndex * 3]];

    float3 pointOnTriangle = ClosestPointOnTriangle(pos, a, b, c);
    float3 normal = cross(b - a, c - a);
    
    float3 v = pos - pointOnTriangle;
    float3 dirToFace = normalize(v);
    float distToFace = length(v);

    if (dot(dirToFace, normal) < 0)
    {
        distToFace *= -1;
    }

    return distToFace;
}

float SmallestPointDistanceToMesh(float3 pos)
{
    float minAbsoluteDistance = 3.40282347e+38F;
    float minDistance = 3.40282347e+38F;

    for (int i = 0; i < _NumTriangles; i++)
    {
        float distance = EvaluateTriangle(i, pos);
        float absoluteDistance = abs(distance);

        if (absoluteDistance < minAbsoluteDistance)
        {
            minAbsoluteDistance = absoluteDistance;
            minDistance = distance;
        }
    }

    return minDistance;
}

The function I used to find the closest point on a triangle is from the Embree Ray Tracing Repo.

Once the SDFs have been produced, they are sent to the GPU with a 'cutout ID'. Then, submarines can simply register a cutout with a chosen ID with the water system, along with a transformation matrix to remove any water intersecting the submarine. This is done by calculating the world space position of the water surface (and the raymarching function) and multiplying it by the world to local matrix provided. Finally the position is converted to uv coordinates and evaluated against the dictionary.

To avoid sampling the SDF's for every fragment, I also implemented a bounding box check which must be passed before sampling the SDF texture. Cutout instances are also frustum culled to avoid evaluating out-of-view cutouts.